Modul 3
Zurück zu Modul 2, vorwärts zu Modul 4.
Kombination von Sensoren
Bis jetzt haben wir Sensoren dazu verwendet, Objekte rund um den Roboter wahrzunehmen. Nun schauen wir uns eine weit verbreitete Aufgabe an: die Linienfolge. Die Aufgabe ist so beliebt bei Anfängern, da sie alle Komponenten eines «richtigen» Roboters besitzt – es wird ein Sensor verwendet, um Informationen über die Welt zu sammeln, und der Roboter ändert sein Verhalten in Abhängigkeit von diesen Informationen.
Dazu musst du wie im Bild einen Farbsensor gegen den Boden ausrichten. Versuche nun einen solchen Roboter zu bauen.
Roboter zur Linienfolge können mit einem, zwei oder einem Dutzend Farb- bzw. Lichtsensoren ausgestattet werden. Je mehr Sensoren ihr habt, desto besser können die Roboter im Allgemeinen einer Linie folgen. In diesem Beispiel beschränken wir uns auf einen einzelnen MINDSTORMS-Farbsensor.
Stellen wir uns folgendes Szenario vor:
Wir kleben mit schwarzem Klebeband oder Tape eine Linie mit Kurven. Irgendwann stellen wir auf die Linie einen Holzblock. Die Aufgabe ist nun, der Linie zu folgen und exakt 20 cm vor dem Holzblock zum Stehen zu kommen. Wie gehst du vor?
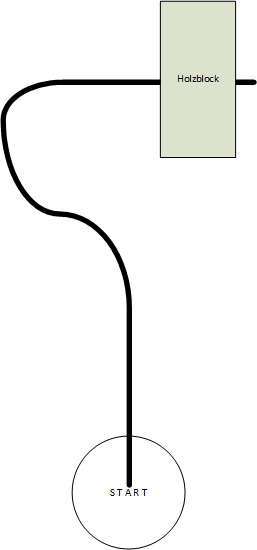
Die Linienfolge
Grundsätzlich ist das Prinzip der Linienfolge rasch erklärt. Wenn wir als Menschen einer Linie folgen, so ist das für uns einfach, da wir vorausschauen und die Linie mit deren Umgebung sehen. Der Roboter sieht nur, ob er auf der Linie ist oder nicht, da der Sensor direkt auf den Boden schaut.
Aus diesem Grund müssen wir mit dem Roboter nicht der Mitte der Linie, sondern dem Rand der Linie folgen. Aber warum?
Wenn wir der Linie selbst folgen, wissen wir nie, auf welcher Seite der Linie wir uns befinden. Sobald der Roboter von der Linie abweicht und der Sensor die Farbe «weiss» sieht, können wir sind sagen, ob wir links oder rechts von der Linie sind.
Wenn wir der Linienkante folgen, wissen wir, dass der Roboter bei einer Abweichung (sieht weiss) links vom Rand der Linie liegt. Wenn er «schwarz sieht», wissen wir, dass er sich gegen rechts bewegt hat. Dieses Prinzip wird als «linker Linienfolger» bezeichnet und ist im unteren Bild zusammen mit dem «rechter Linienfolger» dargestellt.
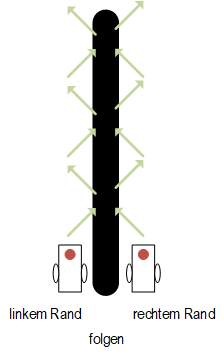
Als Roboterbauer und Programmierer müssen wir wissen, welche Werte der Sensor zurückgibt. Was heisst konkret «weiss sehen» und «schwarz sehen»? Gibt es auch Abstufungen?
Ein typischer nicht kalibrierter Sensor wird einen «weissen» Wert von 50 und einen «schwarzen» Wert von 40 liefern (nicht kalibriert meint hier gesehen auf einer Skala von 0 bis 100). Um sich das besser vorzustellen, haben wir die Sensorwerte in einem Zahlenstrahl visualisiert.
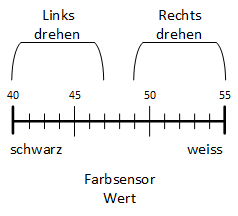
Mit diesem Vorwissen können wir nun mögliche Programmieroptionen für die Linienfolge fortentwickeln. Wir unterscheiden zwischen drei verschiedenen Arten von Linienfolge-Programmen:
- Einfache Linienfolge / weiche Linienfolge
- 3-stufige Linienfolge
- Proportionale Linienfolge / PID Linienfolge
Im Folgenden schauen wir uns alle drei Arten kurz an.
Versuche mit deinem Programmierwissen alle drei Arten zu programmieren und auf einem Parcours zu testen. Bei der PID-Variante zeigen wir dir anhand von Pseudocode, was wir für eine Lösung programmiert haben.
Einfache Linienfolge
Zuerst müssen wir uns entscheiden, ob wir dem linken oder rechten Rand folgen. Im Loop schreiben wir dann: Falls der Sensor schwarz sieht, nach scharf nach rechts drehen, falls der Sensor weiss sieht, scharf nach links drehen. Wir teilen somit die Skala der Farbsensorwerte einfach in zwei gleiche Teile und sagen beispielsweise, dass der Roboter bei einem Wert von weniger als 45 nach links abbiegen soll. Wenn der Wert grösser als 45 ist, soll er rechts abbiegen.
Versucht selbst herauszufinden wie genau die Kurven gemacht werden sollen. Als Tipp geben wir folgendes auf den Weg: verwende sanfte Kurven bzw. Korrekturen für eine eher gerade Linie. Falls einer Linie mit vielen Kurven gefolgt werden muss, versuche schärfere Kurven zu programmieren.
Hier handelt es sich um eine sogenannte 2-stufige Linienfolge, da wir entweder nach links oder nach rechts fahren (2 Möglichkeiten).
Versuche diese Linienfolge zu programmieren. Spiele mit den Werten in der Funktion «RotateMotor()» herum. Was fällt dir auf?
Weiche Linienfolge
Spiele nun so lange mit den Werten für das Fahren und Drehen der Motoren, bis du herausgefunden hast, wie man die Linienfolge weicher gestalten kann und der Roboter trotzdem noch dem Parcours folgt.
Mit dem Austesten wirst du dann bei dieser Art der Linienfolge angelangt sein: Der einzige Unterschied zwischen der einfachen und der weichen Linienfolge, sind die weniger intensiven Ausbrüche des Roboters, wenn der Sensor feststellt, nicht mehr auf der Linie zu sein, d. h. konkret die Veränderung des Winkelwertes.
Versuche nun einer gekrümmten Linie bzw. einer Linie mit verschiedenen Kurven zu folgen. Wie verhält sich deine Linienfolge?
3-stufige Linienfolge
Bei dem vorherigen Ansatz (2 Stufen) fährt der Roboter niemals gerade, selbst wenn er perfekt auf der Linienkante ausgerichtet ist und die Linie gerade ist. Das scheint nicht sehr effizient zu sein, oder?
Nun bauen wir eine dritte Stufe in den Code ein: Falls sich der Wert des Farbsensors zwischen 44 und 47 bewegt, fahren wir mit beiden Motoren gleich schnell (geradeaus). Dadurch haben wir noch weniger Zickzack-Kurs.
Versuche nun mit dieser Linienfolge einer Kurve zu folgen, was stellst du im Vergleich zur weichen Linienfolge fest?
Wir können jedoch festhalten, dass dieser Ansatz besser als der 2-stufige funktioniert. Zumindest bewegt sich der Roboter jetzt manchmal geradeaus.
Ihr denkt nun wahrscheinlich: «Gut, wenn drei Wertebereiche besser als zwei sind, wie wäre es, wenn wir noch weitere hinzufügen?» Mit dieser Überlegung sind wir bereits bei der proportionalen Linienfolge.
Proportionale Linienfolge / PID Linienfolge
Ein PID-Regler (proportional-integral-derivative controller) ist eine gängige Technik, die zur Steuerung einer Vielzahl von Maschinen, einschliesslich Fahrzeugen, Robotern und sogar Raketen, verwendet wird. Die vollständige mathematische Beschreibung eines PID-Reglers ist ziemlich komplex, aber es reicht aus, ein grundlegendes Verständnis zu haben, um einen PID-Regler effektiv einzusetzen.
Der PID-Regler wird typischerweise für die Linienfolge verwendet. Weitere Anwendungen sind z. B. Roboter, welche so gerade wie möglich fahren sollen, oder «zweirädrige humanoide Roboter», die sich ausbalancieren können.
Was ist nun das «P» in PID? Bei einer proportionalen Linienfolge variiert die Drehung des Roboters gleichmässig zwischen zwei Grenzen. Wenn der Sensor anzeigt, dass wir uns in der Nähe der Linie befinden, machen wir eine kleine Kurve. Wenn wir weit von der Linie entfernt sind, machen wir eine grosse Korrektur.
Proportional bedeutet auch, dass zwischen zwei Variablen eine lineare Beziehung besteht: d. h. das die Verbindung der beiden Variablen eine gerade Linie erzeugt (wie im folgenden Diagramm rechts).
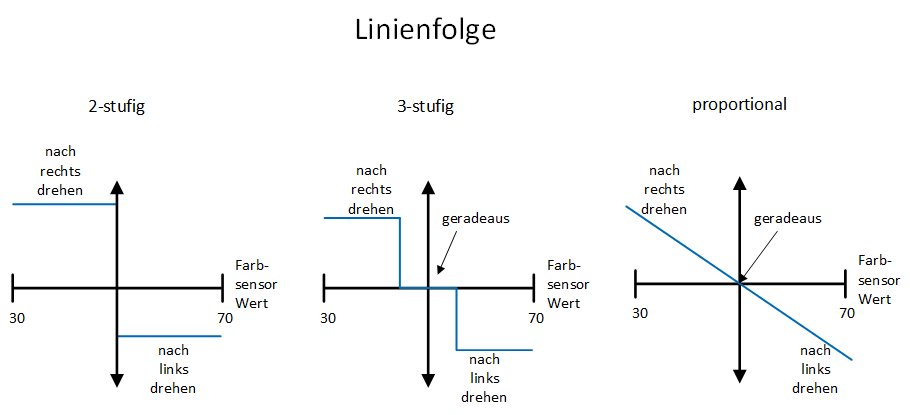
Falls ihr mehr über die mathematische Herleitung eines PID-Reglers Wissen wollt, lest den fantastischen Artikel über PID von Sluka 🇬🇧. Im Folgenden beschränken wir uns primär auf die Erklärung des Programmcodes.
In der Programmierung werden häufig sogenannte Pseudocodes erstellt. Darunter versteht man einen Programmcode, der nicht zur Interpretation durch den EV3-Brick, sondern lediglich zur Veranschaulichung eines Paradigmas, Ablaufes oder Algorithmus dient. Beispielsweise kann ein Coach oder Mentor einen Pseudocode schreiben, damit ihr die Vorgehensweise seht und dies dann konkret nach unserer «Anleitung» programmieren könnt.
Für die proportionale Linienfolge geben wir ebenfalls nur einen Pseudocode vor:
// die drei Variablen initialisieren für unsere proportionale Kurve
Kp = 10 // Konstante für die Berechnung des Korrekturwertes
offset = 45 // Wert um vom Farbsensor-Wert den Korrekturwert zu erhalten
Tp = 50 // Power-Level der beiden Motoren
Loop forever
LightValue = read light sensor // Speicherung des aktuellen Farbsensor Wertes
error = LightValue - offset // Berechnung des Korrekurwertes indem der Offset Wert vom Farbsensor Wert subtrahiert wird
Turn = Kp * error // Wie gross soll die Änderung der Motoren-Geschwindigkeit sein
powerA = Tp + Turn // Motoren-Geschwindigkeit für Motor A
powerC = Tp - Turn // Motoren-Geschwindigkeit für Motor C
MOTOR A direction=forward power=powerA // Ausführen der Funktion zum Vorwärtsfahren mit der ausgerechneten Geschwindigkeit
MOTOR C direction=forward power=powerC // Dasselbe für Motor C
end loop forever // Schleife fertig, wiederholen der AnweisungenPID Linienfolge
Damit die proportionale Linienfolge und somit die Regelung gut funktioniert, müssen drei Bereiche erfüllt sein:
- Der Sensor muss einen grossen Dynamikumfang haben, d. h. er sollte möglichst viele Abstufungen zwischen ganz schwarz und ganz weiss liefern können
- Der Motor sollte ebenfalls im Bereich der Geschwindigkeit einen grossen Dynamikumfang haben
- Das Zusammenspiel von Sensor und Motor muss ohne Verzögerung funktionieren, am besten direkt
Alle drei Punkte sind leider mit unserer LEGO® Hardware nicht gegeben. Es gibt aber auch an der Software noch Verbesserungspotential. Fügen wir nun der proportionalen Linienfolge das I (integral) hinzu.
Das Integral verwenden wir, um die fortlaufende Summe des Fehlers zu erfassen. Es dient als eine Art «Gedächtnis». Dank dem Integral kann der Regler Fehler beheben, die sich über einen «längeren Zeitraum» aufbauen. Mit dem längeren Zeitraum sind dabei mehrere Durchgänge in der Haupt-Schleife des Programmes gemeint.
Nachfolgend der komplette Pseudocode. Nun sind nur noch die neu dazugekommenen Zeilen im Code kommentiert. Viel Spass beim Nachprogrammieren.
Kp = 1000 // WICHTIG wir rechnen Kp*100 d. h. die Zahl ist 10!
Ki = 100 // WICHTIG wir rechnen Ki*100 d. h. die Zahl ist 1!
Kd = 10000 // WICHTIG wir rechnen Kd*100 d. h. die Zahl ist 100!
offset = 45
Tp = 50
integral = 0 // Initialisierung des Integrals
«I-Regler»
lastError = 0 // Initialisierung des mitlaufenden Fehlers
derivative = 0 // Initialisierung des Differenzierer
«D-Glied»
Loop forever
LightValue = read light sensor
error = LightValue - offset
integral = integral + error // Berechnung des Integrals
derivative = error - lastError // Berechnung des Differenzierer
Turn = Kp*error + Ki*integral + Kd*derivative // der «P-Regler», der «I-Regler» und das «D-Glied»
Turn = Turn/100 // WICHTIG hier wird der Faktor 100 in den Variablen Kp, Ki und Kd rückgängig gemacht!
powerA = Tp + Turn
powerC = Tp - Turn
MOTOR A direction=forward power=PowerA
MOTOR C direction=forward power=PowerC
lastError = error // aktueller Fehler speichern, damit für nächste Schleife Wert in lastError ist
end loop forever Wie oben erwähnt, könnt ihr alles über die Mathematik dieser Regelung in einfachen Worten im Dokument von Sluka nachlesen. Zudem gibt er Tipps, wie man die einzelnen Variablen verändern kann und was diese Anpassungen für einen Einfluss auf die Linienfolge haben. Grundsätzlich gilt beim Linien folgen – «Learning by doing».
Bonusaufgaben
Aufgabe 5: Verändere das Licht im Raum, wo du die Linien geklebt hast. Was passiert und wieso? Versuche mit dem gleichen Code andersfarbigem Tape/Klebeband zu folgen. Funktioniert dies genau gleich? Wieso nicht?
Aufgabe 6: Versuche ein Programm zu schreiben, welches die vom Boden ausgelesenen Farbwerte direkt auf dem Display des EV3-Brick anzeigt. Schau dir dazu die Funktionen «LcdClean()» und «LcdTextf()» genauer an. Was stellst du bei unterschiedlichen Farben fest?
Aufgabe 7: Schaue dir diese Folien 🇬🇧 vom Team EV3Lessons zur Kalibration von Sensoren an. Schreibe ein ähnliches Programm mit c4ev3.
